Hello friends,
Thank you so much for liking my previous post & even posting your wonderful comments & views on it...
-----
I have been asked about Fractions by people quite often...
Few months back, I had shared my experience of working with a student on Fractions, which was quite appreciated by teachers, parents and even teacher educators. Here it is:
Playing Maths: "It is Half... No, it is 1 Upon 6... No, it is Half... No,it is...."
http://rupeshgesota.blogspot.in/2014/11/playing-maths-it-is-halfno-it-is-one.html
-----
Okay...Something very exciting happened in our class today too (Yes, on Fractions!) and so, I cant wait to share this with you :)
Assessments were done and I was checking their answer papers.....I noticed that a student had used an interesting approach to solve a Fraction Estimation problem that I generally ask to every middle and high school student.....Two other students were working on a math puzzle next to me and so I thought to try this problem with these students... I was curious to know how they would see and solve this problem.
Question: Is ( 9/12 + 1/5 ) greater than 1 or lesser than 1?
I wanted them to solve this problem together and mentally... But they -- Rohit and Sania -- spread out on the two extremes of the blackboard to work out on their own...
Before you look at their work, I would suggest you to solve this problem, on your own :)
.....
....
.....
....
....
....
....
....
....
....
And this is how their work looked like......... after about 2 minutes:
Thank you so much for liking my previous post & even posting your wonderful comments & views on it...
- Thanks for sharing. I love to "see" teachers in action helping kids learn in their own!
- Very nice ! That's the joy of discovery We do not need robots to memorize everything on tips, we need discoverers !!
- An interesting read to let the child learn by analysis of his own possible answers..Needs loads of patience on the part of teachers! Doing a wonderful job..keep it up
Those who have missed it, here's the link for you:
There's seem to be some problem in Table of 15..
http://rupeshgesota.blogspot.in/2016/08/there-seems-to-be-some-problem-in-table.htmlThere's seem to be some problem in Table of 15..
-----
I have been asked about Fractions by people quite often...
Few months back, I had shared my experience of working with a student on Fractions, which was quite appreciated by teachers, parents and even teacher educators. Here it is:
Playing Maths: "It is Half... No, it is 1 Upon 6... No, it is Half... No,it is...."
http://rupeshgesota.blogspot.in/2014/11/playing-maths-it-is-halfno-it-is-one.html
-----
Okay...Something very exciting happened in our class today too (Yes, on Fractions!) and so, I cant wait to share this with you :)
Assessments were done and I was checking their answer papers.....I noticed that a student had used an interesting approach to solve a Fraction Estimation problem that I generally ask to every middle and high school student.....Two other students were working on a math puzzle next to me and so I thought to try this problem with these students... I was curious to know how they would see and solve this problem.
Question: Is ( 9/12 + 1/5 ) greater than 1 or lesser than 1?
I wanted them to solve this problem together and mentally... But they -- Rohit and Sania -- spread out on the two extremes of the blackboard to work out on their own...
Before you look at their work, I would suggest you to solve this problem, on your own :)
.....
....
.....
....
....
....
....
....
....
....
And this is how their work looked like......... after about 2 minutes:
What did you observe?
Let me guess...
1) You were absolutely shocked with the approach used by Rohit, isn't it? :-) :)
2) Sania's method being familiar to you, might not surprised you much...
But Hold On !!
- What if I tell you that -- I have NOT taken any special effort/ class to teach them the "rules or procedure" to add/ subtract the fractions with unlike Denominators?
- We have rather spent enough time in understanding and visualizing the fractions and equivalent fractions.
- We do some fraction arithmetic, but occasionally, and that too in an unconventional / completely informal way whenever we require it in the problems that lead to fractions (of course, not the boring and easier text-book problems :-)
After knowing this background, you would be surprised even with Sania's method, isn't it? :)
Further, when they were asked for explanations, both of them reasoned beautifully -- it was difficult to add the 2 fractions with different denominators, so they tried to make their denominators same... The sum of 2 fractions is less than one because:
- a number is divided by the bigger number (by Sania, while referring to 57/60)
- when both Nr. and Dr. are same, it is whole & here Nr. < Dr. (by Rohit, while referring to 11 2/5 / 12)
I couldn't resist my urge and had to ask Rohit --
"So how much more is needed to make the sum whole?"
"Sir, we need 3/5 more to convert this into whole! 11 2/5 + 3/5 = 12."
Then I asked them to study the method of their peer... They understood each other's approaches...
I asked Sania - "Do you know what have you done with the two denominators?"
"Sir, I have made them equal..."
"Yes, true.... But how did you get the number 60?"
"Since 12 could not be expressed as an integral multiple of 5, I needed another number that was multiple of both 12 and 5.... So I took 60..."
"Hmmm..... Can you see some relation between 12, 5 and 60?"
After studying them for a while, " Sir, 12 x 5 = 60....." There was a sparkle in her eyes!
"Did you know that just multiplying them would give you the desired multiple?"
"No..."
"Can there be number other than 60..?"
"Ummm....... . 120.....?"
" Yes.... One more?"
"....180...."
"So what are you doing? What's happening?"
"Sir, 60, 120, 180.... all the multiples of 60 would be multiples of 12 as well as 5..."
"True... So what's special about 60?"
Rohit intervened -- "Sir, it is the Lowest Common Multiple of 12 and 5..."
Again, there was a big surprise and then even smile on Sania's face :-)
I was desperate to hear this jargon (LCM) from their mouths..... It was such a deep satisfaction to see these students 'Discover' the rule which is unknown (not explained) to most of the students...
"So how would you solve this problem now.... Is 3/7 + 2/3 bigger or smaller than 1?"
Both of them had resorted to the same approach now (making both Dr. equal) :
After working out --
"Their sum is bigger than 1 because 23 > 21"
Though they had impressed me enough, however I wanted to raise the bar...
"Now, can you solve this problem without pen and paper.... I mean, without any kind of simplification that you have just done?"
They gave me a blank face. I understood, that they had not got my question.
"I want you to just estimate their sum, and not calculate their exact sum."
Still a blank face....
"Okay... What if I ask you --- Is 48 + 29 less than 1000 or more than 1000 ?"
"It is more than 1000" - a loud chorus reply.
"Hmmm... Did you actually add 48 and 29 to get this answer?"
I wanted to hear 'No' but what I instantly heard from Rohit was "Yes Sir, I got the question.."
We looked at Sania for her views... After thinking for a while, she was with us.
Rohit - "Sir, 3/7 is smaller than Half."
"How do you know this?"
"Because 1/2 = 3/6 and in 3/7, we have divided 3 by 7 i.e by a number bigger than 6...
Hence 3/7 < 3/6 i.e. 3/7 is lesser than Half..."
I looked at Sania.... "Yes Sir, I agree with Rohit..."
"So what next?", I probe Rohit.
"2/3 is bigger than Half because of the same reason (2/4 = Half)"
"okay.... So what can we conclude about their sum?"
"Sir, it's difficult to predict.... One is bigger and the other is smaller than Half..."
I ask Sania -- "What's the problem Rohit is talking about?"
"Sir, he is right... We don't know how these two fractions will add up... Their sum might be bigger or smaller than one.."
"In what case, it would be easier for us?"
Rohit -- "If both were bigger than half or lesser than half, we can easily predict....."
"Hmm... Good thinking..."
I could have probed them further to do the analysis for this kind of problem; however, for some reason I drew their attention to the very first problem....
"Will you be able to solve the first problem mentally?" (i.e Is 9/12 + 1/5 > 1 )
Rohit looked at the fractions and - " No Sir, here also we face the same problem."
"Plz explain..."
"9/12 > 9/18 i.e. It's more than half....&... 1/5 < 1/2 i.e. It's less than half...So we can't decide here as well.."
"What if we replace the fraction 9/12 by 9/17?"
I write this problem on the board 9/17 + 1/5.... (why did I do so?)
"Sir, here too it's the same problem.... 17 in the Dr. < 18.... If it were more than 18, then this fraction too would be smaller than half like the second one; and their sum would be less than one. But in the given case, we can't say anything.."
"Hmmm......Okay..."
It was high time for me now and I wanted to push them to think beyond their opinion - 'it is not possible to tell in these cases'...
So I thought of a strategy and bounced back on them -
"I know that you have noticed that the two fractions are smaller and bigger than half.... Is it now possible for us to determine the quantity by which they are smaller or bigger than half?"
It was interesting to watch them at this juncture; it seems they had not thought of this idea earlier.
So now, they again went back to their islands, but this time I found them engrossed in just looking at the original two fractions (9/12 and 1/5)... It was a visual delight to see my students meditating in maths !!
After some time, Rohit started scribbling something on the board. On probing, he answered-
"Sir, 9/12 = 6/12 + 3/12....... i.e. 9/12 is 3/12 more than Half."
"Ok.."
"But then 3/12 = 1/4.... and............ 6/12 = 1/2..........."
Yes !!! I was waiting for the bulb to glow now !! :)
"Sir.... then 9/12 becomes 1/2 + 1/4 = 3/4.... It is three-quarters !!"
I could see him shocked at this revelation, as it was least expected by him...
"What surprised you so much Rohit?"
"Sir, I did not know that 9/12 is same as three quarters! "
"Hmm.... you know that's the trap I lay for students..." I exclaimed this proudly and continued -- " Can you now justify as to why 9/12 = 3/4 ?"
"Yes Sir... It is just the simplified equivalent fraction of 9/12.... I feel stupid I did not realize this before... "
Surprise, Embarrassment, Joy --- I could feel all his these three shades at this moment.
"Okay.. let's move ahead.... "
He thought for some time and soon gave a fantastic reasoning that I was dying to hear !!
"Sir, now 9/12 = 3/4..... And we are adding 1/5 to this 3/4......... We know that 3/4 needs 1/4 to become whole...... But we are adding only 1/5 to it, which is smaller than 1/4....... and hence their sum would be less than whole....."
Take some time to digest this explanation and even appreciate this rare reasoning ! :-)
"Good one... Sania, what are your views on this?"
I had ensured that she was witness to our conversations so far. She agreed with Rohit. But I assessed (& ensured) her understanding by asking her couple of questions for my satisfaction.
"So now... Tell me.... Which method of analysis did you like more - the earlier one or this new one?"
Both of them voted for this Mental/ Visual method. !!
"What about our little modified version then : 9/17 + 1/5 ? Will their sum be > 1 ?"
I wanted them to answer this problem instantly now.... (why so desperation?)
(See if YOU can you answer instantly?)
But I was surprised that Rohit stayed mum this time... In fact, both of them were silent for about 20-30 seconds... It was getting hard for me to curb my urge to intervene...esp. after seeing them shine few seconds back....
I switched to Sania this time...
"Yes Sania, what do you feel?"
With little reluctance and low volume -- "Sir, it should be smaller only naa?"
Wow! It seems she had cracked it... But then why is she not confident ....?
"Go ahead dear.... Plz explain why?"
"In this case we are adding the fraction 9/17 to 1/5........
Now, 9/17 is already smaller than 9/12......
So, if 9/12 + 1/5 < 1, then 9/17 + 1/5 should also be < 1......."
I was so glad that she could do what I was yearning for !!
"Good one!! Rohit, do you agree with her views?"
"Yes Sir, I too was thinking on the same lines..."
"Fine, let's get back to the last problem then....Is 3/7 + 2/3 greater than or less than 1?"
And if you feel that this problem too was solved in a similar way, then please Hold on friends.... We had much more fun and acquired more learning in solving this last part as compared to the previous problems..... (how come?)
But it's 2 hrs past midnight now and even this current post has grown quite longer... So, I will share the interesting climax of this story as Part-2 of this post in couple of days..
Please let me know your views, experiences, suggestions and reflections, on this post... You may also share with me as to how You and your students / children would see and solve these fraction estimation problems.. I would love to know from you.....
See you soon.... :-)
Regards
Rupesh Gesota
https://www.facebook.com/rupesh.s.gesota
https://www.facebook.com/program.MENTOR/
PS: The above conversation happened not in English, but in Marathi, because the students belong to marathi-medium municipal school (from challenged socio-economic background) with whom I work regularly. Check the website: www.supportmentor.weebly.com to know more about this program - MENTOR. There's a short video-clip on its homepage.




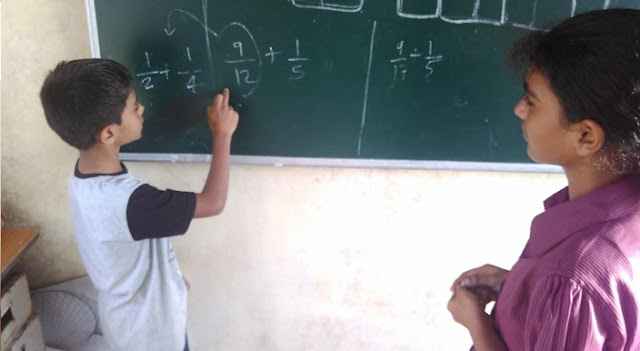


Rupesh this was so wonderful! I had been asked by one kid as to why we need to take the LCM while adding 2 fractions and not so while multiplying them. I guess they wouldn't have asked this had I thought them the way you did. I am just learning how to teach math and hope to see more posts from you. Thank you. :)
ReplyDeleteI am glad you found it helpful... Best wishes..
DeleteLearning in a analytical way, very good.
ReplyDelete