Hello friends,
Yes, I know I have delayed quite a lot in posting this Part-2. So then, what motivated me to sit for it today?
One email reminder from a teacher and one WhatsApp message from a parent inquiring for the follow-up post on Fractions. It was also so encouraging to know from them and other teachers about the discussions they had in their class about the comparison of the fractions after reading my post on fractions. Super-satisfied !!
If you have been yet unable to read the previous (Part-1) of this conversation on fractions, I would suggest you to do so before you read this second part: This is the link:
http://rupeshgesota.blogspot.in/2016/09/playing-with-fractions-part-1.html
Even I had to first read this first part to recollect the incident and sequence of conversations.
So where were we?
Sania and Rohit had done some fraction comparisons/ estimations in a fantastic way... And I had now pushed them further to solve another problem visually/ mentally without using any conventional procedure for simplifications.
This was the question posed to them:
"Fine, let's get back to the last problem then....Is 3/7 + 2/3 greater than or less than 1?"
This is how their work looked like after some time:
If you notice,
a) Sania had figured out the equivalent fraction of 2/3 i.e. 4/6 (what must be going on in her head?)
b) Can you understand what Rohit has done? :-)
...
...
..
...
...
He is still working on 3/7.. .. But he has decomposed the other fraction 2/3 into its two parts : Half and the Remaining part... Can you identify which is Half and which is the Remaining part from those two fractions?
Also, take some time to digest and even appreciate the creativity and flexibility of this young chap! :-)
Meanwhile, Sania had converted the second fraction 3/7 to its equivalent form as before. Not just that, she also explained me that --
"Sir, 3/7 is less than Half by 1/14"
I noticed that Rohit was still struggling with 3/7.... In fact, I was surprised... He had already decomposed 2/3 , then what was stopping him to work out similarly for 3/7?
So I decided to get these two minds together...... Because -
Sania had found the relation of 3/7 with Half AND
Rohit had expressed 2/3 in terms of (strange looking) Half plus something.
So both of them share each others' work so far... After some discussion, I instruct them to start writing the solution systematically by combine their observations on 2/3 and 3/7.
So here they go ---
And after some time,
...
...
....
Notice the top of the image again... This is what I wrote:
20 - 2 + 8
"What will happen to 20 - Will it increase or decrease? Can you tell this to me without calculating the exact answer?" .... (Why would I ask such a question?)
So this question hinted them that they now needed to compare the two little fractions after 1. And they did this correctly.... Again, I was very happy that they did not say 1/14 > 1/6 (something that 10 out of 8 students generally say... Oops, I mean 8 out of 10 students :-)
So then? The road ahead was easy for them..
This was their final stroke --
"Sir, since we are subtracting a smaller number (1/14) and adding a bigger number (1/6) to 1, the final effect would be to increase 1."
Would wait and love to know your views and comments on this post :)
Thanks and Regards
Rupesh Gesota
Yes, I know I have delayed quite a lot in posting this Part-2. So then, what motivated me to sit for it today?
One email reminder from a teacher and one WhatsApp message from a parent inquiring for the follow-up post on Fractions. It was also so encouraging to know from them and other teachers about the discussions they had in their class about the comparison of the fractions after reading my post on fractions. Super-satisfied !!
If you have been yet unable to read the previous (Part-1) of this conversation on fractions, I would suggest you to do so before you read this second part: This is the link:
http://rupeshgesota.blogspot.in/2016/09/playing-with-fractions-part-1.html
Even I had to first read this first part to recollect the incident and sequence of conversations.
So where were we?
Sania and Rohit had done some fraction comparisons/ estimations in a fantastic way... And I had now pushed them further to solve another problem visually/ mentally without using any conventional procedure for simplifications.
This was the question posed to them:
"Fine, let's get back to the last problem then....Is 3/7 + 2/3 greater than or less than 1?"
This is how their work looked like after some time:
If you notice,
a) Sania had figured out the equivalent fraction of 2/3 i.e. 4/6 (what must be going on in her head?)
b) Can you understand what Rohit has done? :-)
...
...
..
...
...
He is still working on 3/7.. .. But he has decomposed the other fraction 2/3 into its two parts : Half and the Remaining part... Can you identify which is Half and which is the Remaining part from those two fractions?
Also, take some time to digest and even appreciate the creativity and flexibility of this young chap! :-)
Meanwhile, Sania had converted the second fraction 3/7 to its equivalent form as before. Not just that, she also explained me that --
"Sir, 3/7 is less than Half by 1/14"
I noticed that Rohit was still struggling with 3/7.... In fact, I was surprised... He had already decomposed 2/3 , then what was stopping him to work out similarly for 3/7?
So I decided to get these two minds together...... Because -
Sania had found the relation of 3/7 with Half AND
Rohit had expressed 2/3 in terms of (strange looking) Half plus something.
So both of them share each others' work so far... After some discussion, I instruct them to start writing the solution systematically by combine their observations on 2/3 and 3/7.
So here they go ---
...
...
....
Though they had understood the relations between 3/7 and half (i.e 6/14) as well as 2/3 and half (i.e. 3/6), it was not so easy for them to substitute these expressions for the original fractions.. I had to do some scaffolding..
You can see some work on the top of the image(board)
When they were struggling to represent 6/14 as 1/2 - 1/14 in the third step, I asked them how can they write 8 in terms of 10?
Can you see how they have added the two Halves to make 1. I was so glad that they did not get 'lost' in the mess (of four fractions :-)
Yes, they were again a bit stuck up at the last step i.e. 1 - 1/14 + 1/6
What did I do at this instant? Teach them? Explain them? ...... No!
The art of teaching is not in explaining or giving answers but in asking right questions !
Notice the top of the image again... This is what I wrote:
20 - 2 + 8
"What will happen to 20 - Will it increase or decrease? Can you tell this to me without calculating the exact answer?" .... (Why would I ask such a question?)
So this question hinted them that they now needed to compare the two little fractions after 1. And they did this correctly.... Again, I was very happy that they did not say 1/14 > 1/6 (something that 10 out of 8 students generally say... Oops, I mean 8 out of 10 students :-)
So then? The road ahead was easy for them..
This was their final stroke --
"Sir, since we are subtracting a smaller number (1/14) and adding a bigger number (1/6) to 1, the final effect would be to increase 1."
Would wait and love to know your views and comments on this post :)
Thanks and Regards
Rupesh Gesota
PS: The above conversation happened not in English, but in Marathi, because the students belong to marathi-medium government school (from challenged socio-economic background) with whom I work regularly...
Check the website: www.supportmentor.wee


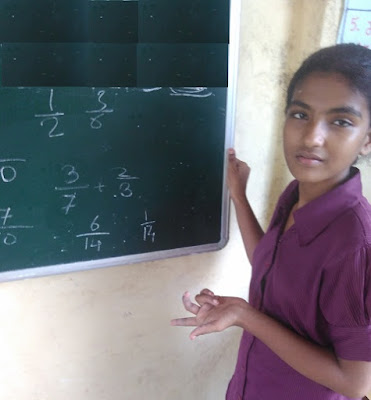



This is a phenomenal way of putting students on a "journey" - i.e. the simple problem in fractions became a small journey for them. Fortunate kids - somebody is willing to spend the time with them to help them discover numbers.
ReplyDelete